Intraday to 1-day Realized Volatility Cone

WTI 10/23/24

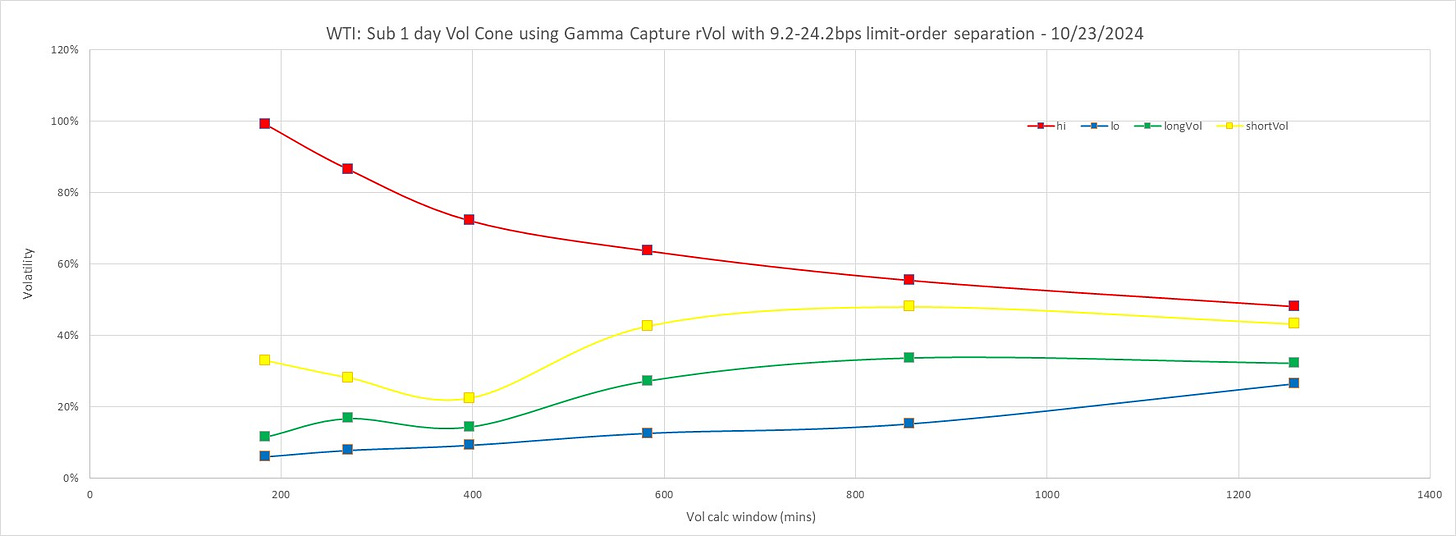
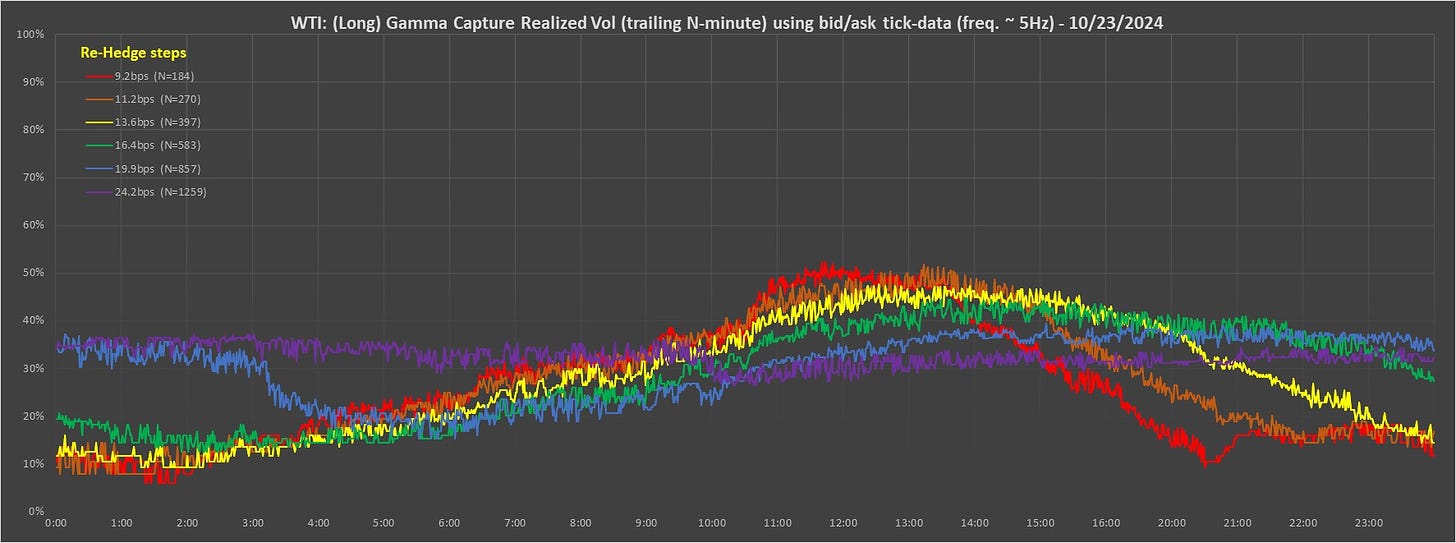
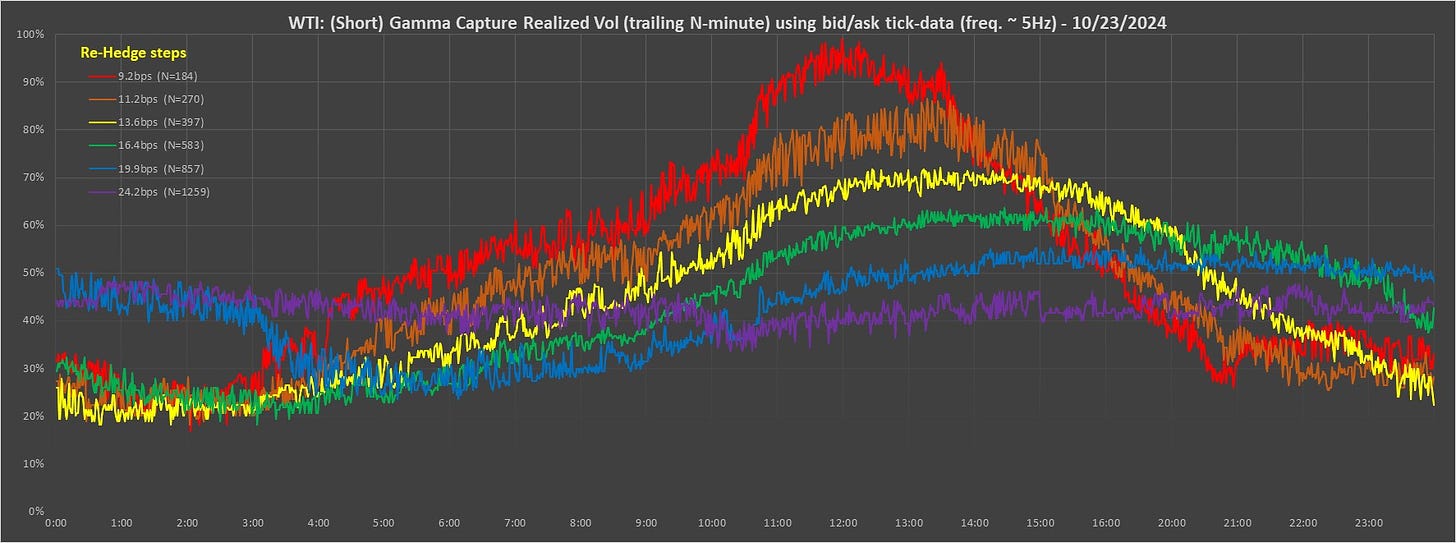
Short-End of the Vol Cone

We use Gamma Capture Realized Volatility (rVol), see below, to value short-dated rVol for various trailing windows, measured in number of minutes. The high and low plus long gamma and short gamma last values are entered into the Vol cone graph for various trailing windows. The size of the re-hedge steps used (again, see below for an explanation of how Gamma Capture rVol works) is chosen to make sure we have about 50 re-hedge executions during the window, to ensure a low variance result (for a static distribution).

This process is similar to the usual vol cone, with various trailing windows for vol calculations, but instead of only considering daily returns, we consider various return sizes to ensure the average contains around 50 component values. This would be analogous to considering various return durations, say daily returns for a 50 day moving rVol estimator using the usual 1-standard-deviation formula, and 2 day returns for a 100 day moving rVol.

Gamma Capture Realized Volatility

The idea is to have a measure of intra-day realized volatility (rVol) that is not critically dependent on assumptions about the security price change process, such as normal returns (log normal price changes) and even allows for jumps.

Method:

1. The above graphs are essentially P&L generation rates for different strategies; let's say different traders.

2. P&L generation rates are not model or even distribution dependent: it's a robust powerful concept for examining market dynamics and micro-structure.

3. The long case is selling at the bid and buying at the ask with limit orders, entered at various constant (bps, 0.01% of price) step separations and indicated in the graph legend with different colors for each step-size/strategy; when a trade gets executed the last-executed limit-order is then re-entered. This maintains a ladder of limit orders. This is the (dynamic-replication) delta-hedging strategy typically executed for a long (constant) Gamma position.

4. The short case (second graph) is selling at the ask and buying at the bid as soon as the price hits the ladder rung levels. This is not quite, but is very similar to, market stop-loss orders (which execute market orders when a trade is registered at the rung level) which are often used to hedge short Gamma positions.

5. Each color line is a different strategy or “trader”. For each strategy, for example, the fastest trader represented by the red line, we count the number of times the re-hedge trade occurs over a trailing period of N minutes, as indicated in the legend, and hence calculate an average rate of re-hedges, i.e., rate of P&L generation. Note that the slowest trader, the purple line, has the widest re-hedge ladder steps and requires the longest averaging period (N minutes) to ensure requisite accuracy/stability.

6. The last step of the analysis is to translate these P&L generation rates into any model variance input, via a decay term. For the lognormal case of the Black-Scholes option model, this translation is

P&L rate = 1/2 * rVol^2 * S^2 * Gamma = 1/2 * (% * S)^2 * Gamma * rate of re-hedges,

i.e., rVol = % / sqrt (average re-hedge time)

The formula rVol = % / sqrt (expected re-hedge time) is derived in these papers[1,2]. These rVols are used for the y-axis (instead of P&L generation rate).

7. Note finally, any model can be used, thus any security can be analyzed, such as interest rates and spreads, which are commonly understood to be not well modeled by lognormal price change distributions, simply by using a different translation from P&L rate to model input parameter(s).

Interpretation:

1. Generally speaking, for a perfectly stable lognormal-distribution (without jumps), the long side shows the rainbow with spaced flat lines from red (fastest trader with tightest re-hedge steps) upwards to purple (slowest trader with largest re-hedge steps). The short side shows higher vols and the opposite; flat lines with from red down to purple. The limit for large re-hedge steps (compared to bid/ask spread size) is that the purple lines will show the same values for long and short. The observed "slippage", i.e., differences from the limiting purple case, is due to "paying" the bid/ask spread. We have posted a few "theo" cases, i.e., using theoretically generated stochastic bid/ask markets to OptionTreeAI substack to illustrate these cases.

2. The second effect is that when jumps occur, or even just sudden increases in rVol, the red line (fast trader P&L) jumps above the (slow trader P&L) purple line, due only to the red line being a shorter averaging time and therefore quicker response.

3. The third effect is that the different strategies do sometimes fundamentally generate different P&L (rVols), even when static, due to market distribution structure not being lognormal. For example, this can be seen after many vol jumps, the red line jumps above purple but stays there for longer than its averaging period: this shows a leading signal of short-term future rVol and the red line (fast) trader is making more money in the long case even though there is slippage. This is a powerful tool for improving P&L when dynamically hedging a book.

Refs:

1. R. Navin, "Measuring Intra-Day Volatility Using First Crossing Time," https://ssrn.com/abstract=4287885

2. E. Sinclair & C. Merrill, "Volatility Estimation via First Exit Times," https://ssrn.com/abstract=3904792

For further information please contact: rob.navin@realtimerisksystems.com

DISCLAIMER

All Options Tree AI materials, information, and presentations are for educational purposes only and should not be considered specific investment advice nor recommendations. Futures, foreign currency and options trading contains substantial risk and is not for every investor. An investor could potentially lose all or more than the initial investment. Risk capital is money that can be lost without jeopardizing one's financial security or lifestyle. Only risk capital should be used for trading and only those with sufficient risk capital should consider trading.